こんばんは、木村陽来です。
今回も、記事をはじめていきたいと思います。

●愛姫、ワタナベミックスについて
愛姫、ワタナベミックスは少しずつですが、成長してきました。

これは火曜日の写真でともに双葉が出ている状態です。
前回、オガタさんに指摘された通り、愛姫にも鉢受けを用意しました。
鉢植えに水が染みだすまで、水をあげます。

ちなみに右上のカイワレ大根が曲がっているのが悲しいですが、ちゃんと緑化ができているので味は問題ないと思います。

●カイワレを食す。
カイワレが程よい長さに育ってきたので、プラスチックコップから取り出しました。
まな板の上に下ろします。

やはり、密度が足らなかったせいか全体的に曲がってしまいました。
しかし、曲がっていても食べることに支障はないはずです。
この日の夕飯は、ナポリタンスパゲッティでした。

噛んでみたところ、シャキシャキとした食感で最初は草みたいな味がするな、と思ったらだんだん辛みが出てきました。
大根なのだから、まあ辛いよな、と思ったら納得できました。おいしかったです。
とりあえず、変な味はしなかったので失敗ではないでしょう。

●長さの計測法について
自分は、カイワレ大根の長さをうまく計測できないことに悩んでいました。
普通に定規を立てると、下の写真のようになってしまうのです。
今は、カイワレが収穫し終わってしまったのでこのボールペンをカイワレと見立てます。
カイワレの種の位置であるはずのところ（ボールペンの根元）を黒く塗っておきます。

プラスチックコップが上に行くにしたがって広がっているので、カイワレと定規の間が空いてしまいます。
これでは正確な長さが計測できません。
そこで、いくつか計測法を考えてみました。

①三角法を用いる。
下の図のような状況を考えます。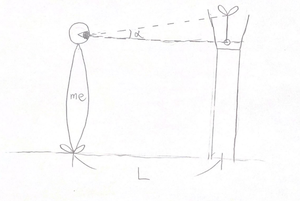

コップの大きさなどは誇張して書いています。
左の「me」と書いてあるのが私です。
私の目の高さと同じ位置に種の高さをそろえ、カイワレ大根の先端を見るときに動かした顔の角度をαとおき、台と自分の距離をLとおきます。
このとき、カイワレ大根の長さをbとおくと、tanα=b/Lなので、b=Ltanαと、カイワレ大根の長さが求められます。

しかし、実際におこなってみてひとつの問題点に気づきました。
角度αを求めることが難しいのです。
最初、横からスマートフォンで、種の部分を見ているときの顔と、カイワレ大根の先端を見ているときの顔を撮影して見比べればいいと思っていたのですが、
手で持って撮影するとずれが出てきてしまいます。
じゃあ、置けばいいのか、と思いましたが、自分の背の高さに合うような台が家になかなかありません。
スマートフォンを吊るす、という案も試しましたが、ビニールひもで吊るすと、スマートフォンがくるくる回転してしまい、やはり安定しません。
そんな感じで、三角法は没になりました。

気を取り直して、次の案を試します。

②影の長さを用いる。
今度は、下の図のような状況を考えます。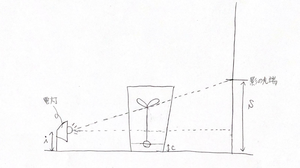

①に引き続き、カイワレ大根の長さをbとします。
また、地面から電灯までの距離をi、地面からカイワレ大根の種までの距離をc、地面から影の先端までの距離をsとします。
このとき、次の簡略化した図を用いると、bが求められます。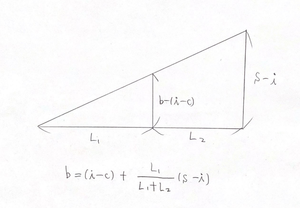

図中にある通り、b=(i-c)+L1(s-i)/(L1+L2)で求められます。

実際に求めてみました。
器具はこんな感じです。

LIGHTの位置に電灯を置きます。
計測したところ、i=2.5cm、c=2.0cm、s=34cm、L1=18cm、L2=27cmでした。
これらの式を上記の式に当てはめると、b=13.1cmになります。
実際のボールペンの長さは14.0cmだったので、なかなか精度が悪いようです。
これでは、普通に定規を立てたときの誤差と大して変わりません。

このままでは終われないので、次週また新しい作戦を考えます。
もちろん、愛姫とワタナベミックスの世話も忘れずに行きましょう。